このホームページに掲載した内容は、過去に趣味で投稿した内容をアップロードしたものです。数学を基礎として発展してきた人工知能や機械学習、シミュレーションなどは、素晴らしい成果を上げてきていますし、今後もますます社会の役に立つと考えられます。このサイトがそれらを学びたい人の一助になれば、幸いです。
投稿者: toughman
[mathjax]
かなり前に「コンボリューショナル・ニューラルネットワークの誤差逆伝播法」をアップしたが、数式ばかりで意味が分かりにくい向きもあるかと思い、図解で分かりやすく説明することにした。
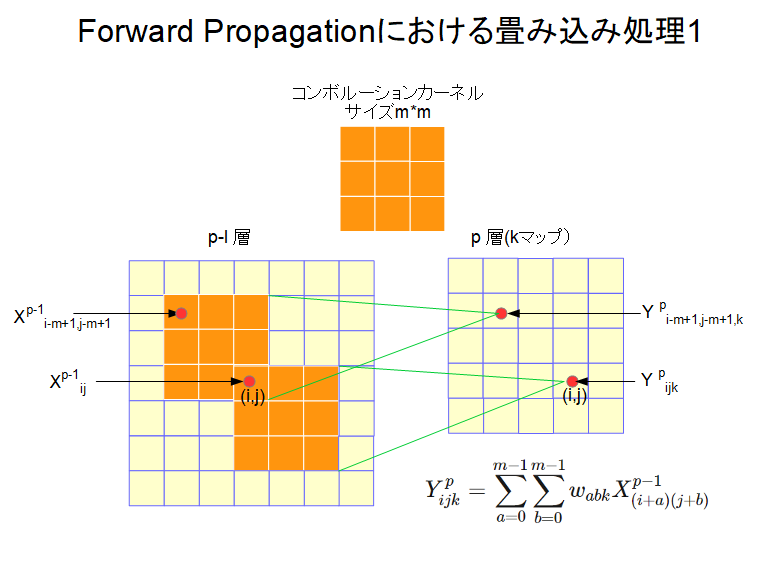
逆伝播を説明するには順方向の伝播をきちんと理解する必要があるので、その説明から始める。図1は順方向のコンボリューション(畳み込み)処理を表している。
\[\begin{eqnarray*}
{Y}_{ijk}^{p} &=& \sum _{ a=0 }^{ m-1 }{ \sum _{ b=0 }^{ m-1 }{ {w}_{abk} {X}_{ (i+a)(j+b) }^{p-1}} }\qquad(1)\\
\end{eqnarray*}\]
\(p-1\)番目のニューラルネットワーク層は、出力\(X_{i,j}^{p-1}\)の2次元配列\((i,j)\)のユニットで構成されている。この層にサイズ\(m*m\)、結合荷重\(W_{abk}\)のカーネルによるコンボリューション処理の計算値\(Y_{i,j,k}^p\)(図1の中に計算式が表示されている)が\(p\)番目のニューラルネットワーク層のユニットへの入力値となることを示している。ここで、kはp層を構成するチャネル(特徴マップ)の番号を表しており、ある一つのコンボルーション層に着目した図であることを意味している。
\(p-1\)層の位置\((i,j)\)にある出力\(X_{i,j}^{p-1}\)は、コンボリューションの開始位置が\((i-m+1,j-m+1)\)と\((i,j)\)を左上と右下の角とする正方形にある場合にコンボリューション処理に取り込まれる。コンボリューションの開始位置が\((i-m+1,j-m+1)\)の場合の計算値\(Y_{i-m+1,j-m+1,k}^p\)はp層の位置\((i-m+1,j-m+1)\)に入力され、コンボリューションの開始位置が\((i,j)\)の場合の計算値\(Y_{i,j,k}^p\)はp層の位置\((i,j)\)に入力される。上記正方形以外の位置を開始位置とするコンボリューション処理には\(X_{i,j}^{p-1}\)は関係しない。この様子を分かりやすく表したのが図2である。
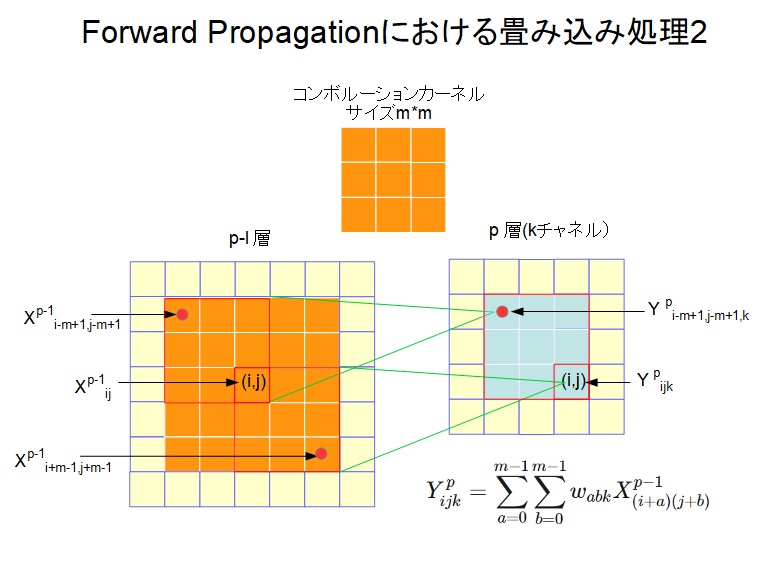
p-1層の\(X_{i,j}^{p-1}\)を含むコンボリューションは図2のp-1層の中に記した橙色の正方形内にコンボリューションカーネルが存在する場合であり、この時の計算値はp層の位置\((i-m+1,j-m+1)\)と\((i,j)\)を左上と右下の角とする正方形に入力される。この正方形が図2のp層内に薄緑色で塗られた領域である。つまり、p-1層の位置\((i,j)\)にある\(X_{i,j}^{p-1}\)はコンボリューション処理によりp層の位置\((i-m+1,j-m+1)\)と\((i,j)\)を角とする正方形の領域に寄与しているのである。
この図式を念頭において、逆伝播を考えてみよう(「コンボリューショナル・ニューラルネットワークの誤差逆伝播法」の式9以下で示した数式がこの部分に相当する)。逆伝播ではp層からp-1層へ誤差を伝播させるが、p-1層の位置\((i,j)\)に影響を与えるp層の範囲は位置\((i-m+1,j-m+1)\)と\((i,j)\)を角とする正方形の領域のみである。この様子が図3に示されており、図3のp層の薄緑色の領域にカーネルサイズ\(m*m\)、結合荷重\(W_{abk}\)のコンボリューション処理をし、その結果をp-1層の位置\((i,j)\)に代入すれば得られる。これは次式で表される。
\[\begin{eqnarray*}
{X}_{ijk}^{p-1} &=& \sum _{ a=0 }^{ m-1 }{ \sum _{ b=0 }^{ m-1 }{ {w}_{abk} {Y}_{ (i-a)(j-b) }^{p}} }\qquad(2)\\
\end{eqnarray*}\]
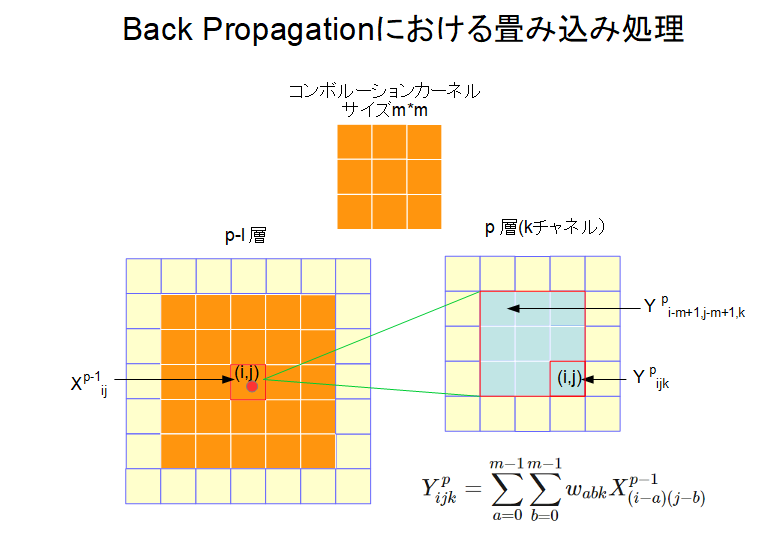
順方向のコンボリューション処理を表す式(1)と逆方向のコンボリューション処理を表す式(2)の違いはコンボリューション処理を掛ける層の下付き添え字が\((i+a,j+b)\)となるか、\((i-a,j-b)\)となるかの違いであり、これはコンボリューション処理を掛ける層のユニット位置が+方向に進むか-方向に進むかの違いを表している(-方向に進む場合、コンボリューションカーネルの要素を上下左右に反転させた\(rot180°\)カーネルを用いると、+方向の通常のコンボリューション処理として表現できる)。言い換えると、順方向の信号伝播も逆方向の信号伝播もともにコンボリューション処理で表せるが、コンボリューション処理を進めるユニット位置の進行方向が逆になる、ということである。この点に留意すれば、両方向への信号伝播が単純なコンボリューション処理で済ませられる。
強化学習 -迷路脱出プログラム-
[mathjax]強化学習が世間の注目を集めるようになったのは、2016年3月に人工知能のアルファ―碁が囲碁の世界チャンピオンを破ってからであろう。囲碁はチェスや将棋などに比べて碁盤のマス目が多く、差し手の選択肢の広がりが膨大で、当分は人間に勝てないだろう、と言われていた。しかし、この予想をくつがえし、強化学習にディープラーニングを適用したアルファ碁は人間の世界チャンピオンを破った。その後もさらに進化し、2016年の年末には世界のトッププロを相手に60戦無敗という圧倒的な強さを示した。とうとう人工知能はここまで到達したのだ。もはや強化学習を知らずして人工知能を語ることはできない。
迷路脱出プログラム(強化学習)
さて、機械学習は大きく分けると、教師あり学習、教師なし学習、強化学習に分類される。この詳細については以前の投稿を参考にして頂きたいが、強化学習はその時点での正解は分からないが、最終的な正解や狙いは分かっている場合に適用される機械学習法である。囲碁の場合も対局の途中では本当の正解の布石はほとんど分からないが、最終的な正解は明確で相手より広い陣地(石で囲んだ範囲)を取ることだ。
この最終的な目的を達成するために、強化学習ではある環境の中にいるエージェント(対象物)を想定する。環境はある「状態」にあり、そこでエージェントはある方策(Policy)に基づいて「行動」をとる。その行動により「状態」は変化し、その結果エージェントは「報酬」を受け取る。その報酬の大小によりエージェントは目的を達成する「行動」を強化していく、というプロセスをとる。
強化学習の代表的な手法としてQ学習法がある。これは以下の手順で学習する。
- 環境の状態を\(s\)、エージェントの行動を\(a\)、行動価値関数を\(Q(s,a)\)(初期値0)、状態の集合を\(S\)、行動の集合を\(A\)とする。\(\forall s=S, \forall a=A\)と表される。
- エージェントは環境の状態\(s_t\)の中にいる。
- エージェントは確率\(ε\)で行動の集合\(A\)からランダムに行動を選択し、確率\((1-ε)\)で行動価値関数を最大にする\( arg \underset { { a }\in A }{ max } Q({ s_t },{ a })\)の行動を選択する。選択した行動\(a_t\)を実行する。
- 行動\(a_t\)により状態は\(s_{t+1}\)に遷移し、報酬\(r\)を受け取る。
- 学習率\(\alpha\)と割引率\(\gamma\)を用いてQ値を以下のように更新する。
\[\begin{eqnarray*}
Q(s_t,a_t)\leftarrow (1-\alpha )Q(s_t,a_t)+\alpha {\delta}_{t} \qquad (1) \\
{\delta}_{t} \equiv r+\gamma \underset { { a }\in A }{ max } Q({ s_{t+1} },{ a }) \quad\qquad (2)
\end{eqnarray*}\] - 時間ステップ\(t\)を\(t+1\)に進め、手順2から繰り返す。
手順3では、確率\(ε\)でランダムに行動を選択し、確率\(1-ε\)で行動価値関数を最大にする行動を選択している。この方策は\(ε\)-greedy方策と呼ばれており、学習回数の増加とともに\(ε\rightarrow0\)となるようにスケジューリングすれば、行動選択は最適方策に近づいてゆく。
強化学習は応用範囲が非常に広い機械学習法で、囲碁や将棋のみならず、インベーダーゲームや対戦ゲームの操作方法、あるいは自転車の乗り方や二足歩行のバランスの取り方など、様々な分野に応用できる。今後ますます利用が広がりそうなテーマなので、是非とも理解しておきたい項目である。
そこで今回はその手始めとなる迷路脱出のプログラムを上記の手順に基づいて作成した(C++)。それが冒頭のビデオである。学習率\(\alpha=0.5\)、割引率\(\gamma=0.99\)、確率\(ε=0.5\)、学習回数200回(エピソード)、1エピソードでの最大ステップ数は1000とし、そこでスタートに戻り次のエピソードを開始させた。報酬はゴールに入れば10000ポイント、スタートに入れば-100ポイント、その外は全て-1ポイントとした。溝に落ちた場合は落ちる前の位置に戻すだけで、報酬は-1ポイントのままにした。溝に落ちることを防ぐと早くゴールにたどり着くので、そのペナルティはあえて科していない。確率\(ε\)の初期値は0.5としたが、1エピソード毎に0.9を乗じて手順3におけるランダムな行動を徐々に減らし、行動価値関数を最大にする行動を採用するようにした。従って、最初は溝に落ちまくっているが、学習回数が増えるに従い、溝に落ちなくなり、ゴールに早く到達するようになる。ビデオの上端に表示した「EPISODE」は学習回数を表示している。0は初回で、40回の学習毎にビデオ表示するようにした。最後にビデオタイトルが「EPISODE ○○」ではなく「Labyrinth」と表示されるが、これは学習200回を終えた後、テスト走行させた時の様子を示している。
迷路の構造は簡単に変えられるように、下のような配列を用いた。数値4が通路で、数値0は溝、スタート(s)は1、ゴール(G)は3とした。
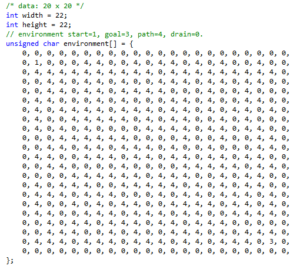
どのような迷路の形を作成しても、着実に学習して全てゴールに辿り着いた。もちろん、スタート点とゴール点が近いと早くゴールに辿り着く。ゴールに到達した時の報酬の値は10000ポイントとしたが、これは10や100、1000にしてもほとんど変わりはなかった。
この迷路脱出のプログラムの動作を見て、私は努力の大切さを思い知らされたような気がした。人間であれば溝に落ち続けてゴールにたどり着けない場合、あきらめて止めてしまうが、コンピュータは延々と脱出口を求めて学習し続けることができる(当たり前だが)。この無限に近い学習過程を取ることが出来る点において、強化学習は秀逸である。
[mathjax]従来のニューラルネットワークの誤差逆伝播法に関してはすでに解説したので、今回はディープラーニングでよく用いられるコンボリューショナル(畳み込み)ニューラルネットワークの誤差逆伝播法(Back Propagation)について解説する。
コンボリューショナルニューラルネットワークの構造を解説した投稿の図2を念頭に置きながら、以下の式の意味を理解して頂きたい。
先ず、\(p-1\)番目の層は2次元配列\((i,j)\)のユニットで構成された、出力\(X_{i j}^{p-1}\)のコンボリューション層であり、\(p\)番目の層はチャネル数を表すk座標にe枚の特徴マップを持つ層とする。コンボリューションのカーネルサイズをm×m、カーネルの2次元座標を\((a,b)\)、結合荷重を\(w_{abk}\)とすると、\(p\)番目の層への入力\({Y}_{ijk}^{p}\)と出力\({X}_{ijk}^{p}\)は式(1)、(2)で表される。
\[\begin{eqnarray*}
{Y}_{ijk}^{p} &=& \sum _{ a=0 }^{ m-1 }{ \sum _{ b=0 }^{ m-1 }{ {w}_{abk} {X}_{ (i+a)(j+b) }^{p-1}} }\qquad(1)\\
\\X_{ijk}^{p} &=& f(Y_{ijk}^{p}) \qquad \qquad \qquad (2)
\end{eqnarray*}\] ここで\(k\)は特徴マップの枚数のインデックスであるので\(0~e-1\)の値をとる。fは非線形活性化関数を表している。\(p-1\)番目の層がd枚の特徴マップで構成される場合は、式(1)は次式のようになる。
\[{Y}_{ijk}^{p}=\sum _{ c=0 }^{ d-1 }\sum _{ a=0 }^{ m-1 }{ \sum _{ b=0 }^{ m-1 }{ {w}_{abck} { X }_{ (i+a)(j+b)c}^{p-1} } }\qquad(3)\]ここで\(c\)は\(p-1\)番目の層の特徴マップのインデックスを表す。式(3)は式(1)と同様の形をしているので、以下では簡単のために\(d=1\)の場合である式(1)を例として話を進める。
【結合荷重の更新方法】
誤差逆伝播法では各層の出力の誤差を\(E\)とすると、1回の学習における結合荷重の微小更新量\(\Delta {w}_{abk}\)は学習率\(\eta\)を用いて次式のように設定される。
\[\Delta {w}_{abk} = -\eta\frac {\partial E}{ \partial {w}_{abk}} \qquad (4) \] コンボリューションを行う層のユニット数がN×Nで構成されているとすると、コンボリューションのカーネルが移動できるユニット数は(N-m+1)×(N-m+1)となる。これら全てが結合荷重\({w}_{abk}\)で重み付けされているので、式(4)はChain rule(連鎖法則)により次のように変形される。
\[\begin{eqnarray*}
\Delta {w}_{abk} &=& -\eta \frac { \partial E }{ \partial {X}_{ijk}^{p}} \frac { \partial {X}_{ijk}^{p}}{ \partial {Y}_{ijk}^{p}} \frac { \partial {Y}_{ijk}^{p} }{ \partial {w}_{abk}} \qquad(5)\\
\\&=& -\eta \frac { \partial \sum _{ i=0 }^{ N-m }{\sum _{ j=0 }^{ N-m }{E }}}{ \partial {X}_{ijk}^{p}} \frac { \partial {X}_{ijk}^{p}}{ \partial {Y}_{ijk}^{p}} \frac { \partial {Y}_{ijk}^{p} }{ \partial {w}_{abk}} \qquad(6)\\
\\&=& -\eta \sum _{ i=0 }^{ N-m }{ \sum _{ j=0 }^{ N-m }{ \frac { \partial E }{ \partial {X}_{ijk}^{p}} \frac { \partial {X}_{ijk}^{p}}{ \partial {Y}_{ijk}^{p}} \frac { \partial {Y}_{ijk}^{p} }{ \partial {w}_{abk}}}} \qquad(7)\\
\\ &=& -\eta \sum _{i=0}^{N-m}{ \sum _{ j=0 }^{ N-m }{ \frac { \partial E }{ \partial {X}_{ijk}^{p}} \frac { \partial \left( f\left( {Y}_{ijk}^{p} \right)\right)}{ \partial {Y}_{ijk}^{p}} \cdot {X}_{ (i+a)(j+b)}^{p-1}}} \qquad(8) \\
\\ &=& -\eta \sum _{i=0}^{N-m}{ \sum _{ j=0 }^{ N-m }{ \frac { \partial E }{ \partial {X}_{ijk}^{p}} f^{ \prime }\left( {Y}_{ijk}^{p} \right) \cdot {X}_{ (i+a)(j+b)}^{p-1}}} \qquad(9)
\end{eqnarray*}\]ここでは式(1)を偏微分して得られる次式(10)を用いた。式(1)にあるサメーションが外れているのは、特定の\(a,b\)を持つ\({w}_{abk}\)で微分しているので、それ例外の\(a,b\)を持つ項の微分がゼロとなるからである。
\[X_{(i+a)(j+b)}^{p-1}=\frac { \partial {Y}_{ijk}^{p} }{ \partial {w}_{abk} } \qquad(10)\]
式(9)の\(X_{(i+a)(j+b)}^{p-1}\)はフォワードプロパゲーションの時に得られる値であり、\(f^{ \prime }\left( {Y}_{ijk}^{p} \right)\)は微分した活性化関数に入力値を代入すれば得られる値で、共に既知である。p層への入力値\({X}_{ijk}^{p}\)による微分誤差\(\partial E/\partial {X}_{ijk}^{p}\)は、出力層の出力と教師画像との二乗誤差の微分値を最初の値とし、それを前の層に順番に逆伝播して利用するものである。これを前の層に順番に逆伝播させることで順次取得できる。\(\partial E/\partial {X}_{ijk}^{p}\)を\({ \delta }_{ i,j }^{ p }\)と記載すると、式(4)は次式となり、荷重結合の微小更新量を得ることができる。
\[\Delta {w}_{abk} = -\eta\sum _{i=0}^{N-m}{ \sum _{ j=0 }^{ N-m } {{ \delta }_{ ij }^{ p } f^{ \prime }\left( {Y}_{ijk}^{p} \right) \cdot {X}_{ (i+a)(j+b)}^{p-1}}} \qquad(11)\]
ここで注意したい点がある。それはコンボリューション処理を経由してp層からp-1層へ\(\partial E/\partial {X}_{ijk}^{p}\) (=\({ \delta }_{ i,j }^{ p }\))を逆伝播する方法である。少しわかりにくい点があるので、以下で解説する。
【コンボリューション層での誤差逆伝播法】
p番目のコンボリューション層はe枚の特徴マップで構成されているので、p-1番目の層の微分誤差は次式のように展開される。
\[\begin{eqnarray*}
\frac { \partial E }{ \partial {X}_{ij}^{p-1}} &=& \sum _{c=0} ^{e-1} \sum _{a=0} ^{m-1}{ \sum _{b=0}^{m-1}{ \frac {\partial E}{\partial {X}_{(i-a)(j-b)c}^{p} } \frac { \partial {X}_{(i-a)(j-b)c}^{p} }{ \partial {Y}_{(i-a)(j-b)c}^{p}} \frac { \partial {Y}_{(i-a)(j-b)c}^{p} }{ \partial {X}_{ij}^{p-1}} }} \quad(12) \\
\\ &=& \sum _{c=0} ^{e-1} \sum _{a=0} ^{m-1}{ \sum _{b=0}^{m-1}{ \frac {\partial E}{\partial {X}_{(i-a)(j-b)c}^{p} } f^{ \prime }\left( {Y}_{(i-a)(j-b)c}^{p} \right) \cdot {w}_{abc}}} \quad(13)
\end{eqnarray*}\] ここでは式(2)と、式(1)を\(X\)で偏微分して得られる式(11)を用いた。
\[\frac{\partial{Y}_{(i-a)(j-b)c}^{p}}{\partial{X}_{ij}^{p-1}} = w_{abc} \qquad(14)\]p番目の層の\(Y\)や\(X\)の添え字が\(i-a\)や\(j-b\)と表記されているが、式(1)におけるp-1番目の層の\(X\)の添え字\(i+a\)や\(j+b\)と符号が逆になっている。これはフォワードプロパゲーションの畳み込み演算において、p-1番目の層の座標\((i+a,j+b)\)がp番目の層の\((i,j)\)に対応しているので、p-1番目の層の座標\((i,j)\)はp番目の層の\((i-a,j-b)\)に対応するからである(詳しい説明を「コンボリューション層の誤差逆伝播法の図解説」で行っているので、参考にしてください)。
式(10)の\(\partial E/\partial {X}_{(i-a)(j-b)c}^{p}\)はp番目の層の微分誤差であり既知であるので、前の層に逆伝播される\(\partial E/\partial {X}_{ijk}^{p-1}\)が求められる。
コンボリューション層の誤差逆伝播式は式(12)などに表されるように、サメーション\(\sum\)を複数用いるので、何をしているのか分かりにくいかもしれない。しかし、ここで行っている誤差逆伝播は従来のニューラルネットワークの誤差逆伝播と本質的に同じである。結合荷重で結ばれているユニット間で誤差を伝播しているだけである。ただコンボリューション層では一つの結合荷重が複数のユニット間を結合しているので、それらの誤差を積算しなければならない。そのためにサメーション\(\sum\)が複数個使われることになる。
コンボリューショナルニューラルネットワークでは、マックスプーリング層が用いられることが多いが、この層は単にコンボリューション層のユニットを一定サイズのブロックに区分し、各ブロック内の最大値を持つユニットを抽出する役割を果たす。従って、誤差逆伝播ではプーリング層のユニットをコンボリューション層の各ブロックの最大値を持つユニットに結びつけるだけでよい。
以上のようにして、コンボリューショナルニューラルネットワークに関する誤差逆伝播を計算することができる。
前の投稿ではニューラルネットワークとディープラーニングの構造を比較した。そこでは手書き数字画像(幅28画素*高さ28画素の白黒画像)を認識する場合を取り上げた。今回はその構造の違いにより性能がどのように異なるのかを説明する。
まず、前の投稿で示したニューラルネットワークとディープラーニングの画像認識プログラムをC++言語で作成した。機械学習の理論に基づいて、全てのプログラムを自作した。手書きの数字画像はMNISTのデータベースを使用した。ここには7万画像が含まれているので、トレーニングに6万画像、性能テストに残りの1万画像を使った。トレーニングに使った画像は性能テストには使用しないことが、正しく性能を評価する上で重要である。
図1にニューラルネットワーク(MLP:多層パーセプトロン)の場合のトレーニング回数(Training Epochs)と性能テストの正解率(Correct Rate)の関係を示す。トレーニングにおいては、6万枚の画像からランダムに画像を選び、画像1枚を入力する毎にバックプロパゲーションにて結合荷重を更新した。
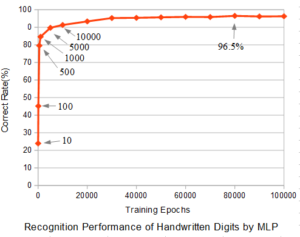
トレーニングパラメータとして学習率ETA=0.01 とした。図中の←10、←100、←500、←1000などはトレーニング回数を表す。認識するのは数字0~9の10文字なので、全くデタラメに回答した場合の正解率は10%となるが、わずか10回学習するだけで、正解率が24%になり、100回で45.2%、1000回で84.6%と急速に向上する。このように正解率が急速に向上するのは、バックプロパゲーションによる学習(結合荷重の更新)が効果的になされていることを示している。
トレーニング1万回では91.3%、3万回で95.4%となり、その後、正解率は横這いとなる。8万回の時に最高値96.5%となっているが、約6万回以降、トレーニング毎の結合荷重の更新で正解率が微小に振動しているので、その影響で最高値が出たと考えられる。トレーニングに使える画像が6万枚であるので、トレーニング回数も6万回程度で飽和するのはもっともなことだと考えられる。トレーニングに使用した画像が似たような画像ばかりであれば、もっと少ないトレーニング回数で正解率が飽和することもあり得る。
次にディープラーニング(CNN:コンボリューショナルニューラルネットワーク)による手書き数字の認識正解率とトレーニング回数のグラフを図2に示す。用いたデータは上記と同じMNISTデータである。
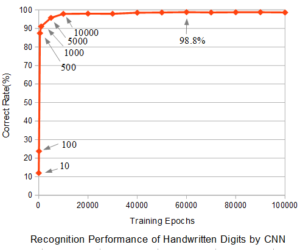
ディープラーニングのトレーニングパラメータとして、学習率ETA=0.01、バッチサイズ10、Momentum=0.1、L2=0.001とした。ドロップアウトは用いていない。バッチサイズ10とは10枚の画像で1回結合荷重を更新することを意味する。
図2でも最初のトレーニングで急速に正解率が向上しており、バックプロパゲーションによる学習が適切に行われていることが分かる。1万回程度のトレーニングで正解率は横這いとなるが、それ以降ほんのわずかずつ向上し、6万回では最高値98.8%の正解率を出した。しかし、このあたりではMLPによるトレーニングと同様に、結合荷重の更新毎に正解率は微小に振動している。また、パラメータの値を変えたり、あるいはCNNの層構造やカーネルのサイズを変えると、正解率も変わるので、いろいろ工夫することで、さらに良い正解率を達成することも十分可能である。
以上のように、従来のニューラルネットワークと最近注目されているディープラーニングの基本的な構造でその性能を比較した。画像認識の性能はそれぞれ96.5%と98.8%となり、2%の差が出た。100%に近いレベルにおいて2%の差が出るということは結構な性能向上と言ってよいであろう。私もこのMNISTのデータを目視で少しだけ認識したが、実は判断のつかない画像が散見された。図3はMNISTデータの一例だが、数字が何なのかを認識するのは簡単ではない。

図3の各数字の右上と右下に小さい数字が記入されているが、右上が正解で右下が間違いの例である。人間でも判断できない数字も少なくない。このような判別が難しい手書き数字の認識において正解率が98.8%あれば、まあま優秀と言えるのではないだろうか。画像認識プログラムは学習データだけを基準として判断するので、人間のような思い込みや自分の癖などが反映されない。よって、人間より客観的な判断ができると言える。
このような画像認識が可能となったディープラーニングは今後益々様々な用途に利用されていくことは間違いなさそうだ。
ディープラーニングはニューラルネットワークの一形態であり、その層数を深くした構造を持つが、単に層数を深くしただけではなく、入力画像の形状を捉えるための工夫が施されている。今回はその構造について説明する。
まず、画像を認識する従来の基本的なニューラルネットワークの構造を図1に示す。これは多層パーセプトロンと呼ばれるニューラルネットワークで、この例では入力層1層、中間層であるHidden層1層、出力層1層の3層構造を有している。
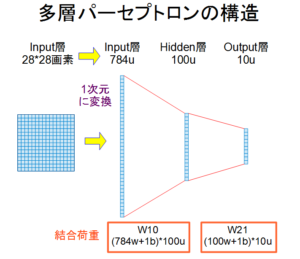
Input層には写真などの2次元の画像が用いられるが、図1に示したように、2次元の画像は1次元に変換されて、入力される。この2次元から1次元への変換は、2次元の各行を単純に1行につないで並べるだけの変換である。
手書き数字(0~9)画像の代表的なデータベースであるMNISTを用いて画像認識を行う場合を例にとれば、Input層は手書き数字の画像サイズ28画素×28画素=784ユニットとなる。Hidden層には100ユニット程度が用いられるケースが多い。最後のOutput層は認識する数字の種類0~9の数と同じになるので、10ユニットとなる。つまり、入力画像が「0」であれば出力層の上から1番目のユニットの出力値が最大となり、入力画像が「1」であれば上から2番目のユニットの出力値が最大、「2」は3番目、「3」は4番目、、、「9」は10番目のユニットの出力が最大となるように機械学習させる。
ニューラルネットワークを作成する上での重要なポイントは結合荷重の設定である。図1の下の方に具体的な結合荷重の数を示した。W10は入力層とHidden層の間、W21は出力層とHidden層の間の結合荷重である。添え字wは荷重パラメータであり、添え字bはバイアスパラメータを示す。初期値にはランダム値が設定される。
このように従来のニューラルネットワークでは、図1のようなシンプルな層構造を持っている。
これに対し、ディープラーニングで画像を認識させる場合には、図2のような構造を取る。

ここでは画像認識で最も高い性能を上げているコンボリューショナルニューラルネットワークで手書き数字画像を認識する場合の一例を示した。図2に上の方に青い枠で囲まれた部分がディープラーニングの構成層を示し、その下の緑色の枠で囲まれた部分が演算に用いるフィルターである。その下に層を構成するユニットの模式図が描かれており、そのユニット数が紫色の下線を持つ数字で示されている。一番下のオレンジ色で囲まれた部分が各層間の結合荷重の構成を示している。
これらを具体的に説明する。図2の上の方で青い枠に囲まれている各層は、Input層、特徴マップ層Fmap1、MaxPoolingされた層S1、特徴マップ層Fmap2、全結合層HiddenF3、Output層で構成されている。
Input層には2次元画像28*28画素をそのまま使う。特徴マップ層Fmap1の1ユニットはInput層に5*5画素の畳み込みカーネルConv-karnelフィルタを掛けることで算出される。Input層28*28の画像の上に橙色の正方形で示されているカーネル領域を左から右に順番に移動させて、Fmap1の全てのユニットの値を算出する。Fmap1は4枚で構成されているので、この操作を4回繰り返して、4枚のFmap1を算出する。同じ操作を4回繰り返して4枚のFmap1を生成するが、演算に用いる結合荷重が異なるので、4枚のFmap1は全て異なる値を持つ。結合荷重の初期値はランダムに設定される。機械学習の過程では教師データの値をフィードバックするバックプロパゲーションにより結合荷重の値が更新される。
このようにして生成されたFmap1層に2*2ユニットのMaxPooling処理をして、S1層を算出する。2*2ユニットのMaxPooling処理とは、縦2横2のユニットの中の最大値をS1層に代入する処理のことである。そのため、S1層のサイズはFmap1の縦横の半分になり、面積としては1/4になる。MaxPooling処理では、特徴マップの枚数に変化はないので、Fmap1が4枚なら、S1も4枚となる。
特徴マップFmap2はS1に対し、5*5*4fのConv-karnelで畳み込み処理をして算出される。ここで5*5*4fは5*5ユニット×特徴マップ4枚の畳み込み演算のことであり、4枚で構成されているS1の同じ位置の5*5ユニットに対して畳み込み処理を行っている。つまり3次元ユニット5*5*4fの畳み込み演算を行っている。ここでFmap2は特徴マップとして8枚を持つ構成にしたので、8枚分同じ処理を繰り返す。ここでも結合荷重の値が異なるので、異なる値を持つFmap2が8枚作製されることになる。
S2はS1とまったく同様なMaxPooling処理である。
このような処理の後、従来のニューラルネットワークのHidden層と同様な全結合層HiddenF3(100ユニット)を設け、これにS2の全ユニットを結合する。この全結合層にHiddenという名前を付けたのは従来のニューラルネットワークと同様の層であるためであり、この層だけがHiddenn(隠れた層)という訳ではない。最後のOutput層と全結合層を全て結合する。
各層をつなぐ結合荷重を図2の下の方に橙色で囲んだW10、W21、W32、W43などで示した。ここで添え字のfは特徴マップ(feature map)の枚数を意味している。
図1のニューラルネットワークと図2のディープラーニングを比較するとよく分かるが、ディープラーニングは従来のニューラルネットワークのInput層とHidden層の間に、畳み込み演算とMaxPooling処理をする数層を挟んだ構造をしている事に大きな特徴がある。
これらの構造の差により、画像認識の性能がどの程度変わるのかを次に解説する。
3次元空間の回帰直線の求め方
[mathjax]2次元平面上に存在する複数の点からその回帰直線を最小二乗法で求める問題はよくあるが、3次元空間に存在する複数の点からその回帰直線を最小二乗法で求める問題はあまり見ないようなので、ここにその解法を書いておきます。
原点を\(O\)とする3次元座標系において、点\({ P }_{ 0 } ({ x }_{ 0 },{ y }_{ 0 },{ z }_{ 0 })\)から点\(P (x,y,z)\)に至るベクトル\(\vec {P_0P}\)(これが求める直線)とすると、ベクトル\(\vec { OP }\)は次式で表される。
\[
\begin{array}{c}
\vec { OP } ={ \vec { O{ P }_{ 0 } } }+\vec {P_0P} \qquad (1) \\
\vec { OP } ={ \vec { O{ P }_{ 0 } } }+t\vec {e} \qquad (2)
\end{array}
\]
ここで、\(\vec {P_0P}=t\vec {e}\)であり、\(t\)はベクトル\(\vec {P_0P}\)の長さ、\(\vec {e}\)は\(\vec {P_0P}\)の単位ベクトルである。
\(\vec {e}\)の成分を\((a, b, c)\)とすると、点Pの各座標は
\[
\begin{array}{c}
x = x_0 + at \qquad (3) \\
y = y_0 + bt \qquad (4) \\
z = z_0 + ct \qquad (5)
\end{array}
\]
となる。ただし、\(a^2+b^2+c^2=1\)。
方向単位ベクトル\(\vec {e}\)のz軸方向の成分が\(0\)でない、つまり\(c≠0\)ならば式(5)から
\[t = (z_0-z) / c \qquad (6)\]となる。
もし、z軸方向の成分が\(0\)、つまり\(c=0\)ならばベクトル\(\vec { t }\)が示す直線は\(x,y\)平面上にあるので、通常の2次元平面上の直線となり、普通の最小二乗法で解を求めることができる。
さて、式(6)を(3)、(4)に代入すると式(7)、(8)が得られる。
\[
x = Az + B \qquad (7)\\
y = Cz + D \qquad (8)\\
y = Ex + F \qquad (9)
\]
式(7)、(8)から\(z\)を消去して\(x,y\)の関係式(9)を算出した。ここでは、\(A=a/c、B=(x_0-Az_0)、C=b/c、D=y_0-Bz_0\)と置き換えている。
式(7)、(8)、(9)はそれぞれ\(zx\)平面、\(zy\)平面、\(xy\)平面における直線式を表している。
この各々の2次元平面において、以前書いた擬似逆行列で回帰直線を求める方法を用いて式(7)、(8)、(9)の係数6個を求める。
つまり、3次元空間に存在する全ての点\((x,y,z)\)の中から、\((x,z)\)の座標を式(7)に入れて係数\(A,B\)を求め、\((y,z)\)の座標を式(8)に入れて係数\(C,D\)を求め、\((y,x)\)の座標を式(9)に入れて係数\(E,F\)を求める。
これにより最初に設定した\(P_0\)の未知数3個と、方向ベクトル\(\vec {P_0P}\)の3つの未知数を全て算出できる。なぜならば、\(\vec {P_0P}\)の未知数は、\(t\)の長さとその単位ベクトルの未知数2個であるからだ(\(a^2+b^2+c^2=1\)より未知数は2個)。このようにして擬似逆行列で求めた直線は各点からの距離が近い回帰直線となる。
<補足>
式(3)、(4)、(5)では、\(t\)はベクトル\(\vec {P_0P}\)の長さとし、\(\vec {e}\)を\(\vec {P_0P}\)の単位ベクトルとした。そして、単位ベクトルの条件(\(a^2+b^2+c^2=1\)から、係数を一つ消去することで、未知数が6個であると説明した。
この考え方でよいのだが、より簡単に計算するには、式(5)の\(ct\)→t’と置き換えることで式(3)、(4)、(5)は以下のように書き換えられる。
\[
\begin{array}{c}
x = x_0 + a’t’ \qquad (3′) \\
y = y_0 + b’t’ \qquad (4′) \\
z = z_0 + t’ \qquad (5′)
\end{array}
\]
この式から、未知数は\(x_0, y_0, z_0, a’, b’, t’\)の6個であることが分かる。この後は上式(6)以下と同様に変形して、未知数を算出することができ、3次元空間の回帰直線が求まる。
最近、人工知能という言葉がテレビやインターネットで見られない日はありません。毎日頻繁に人工知能の進歩の状況や、人の仕事が人工知能にとって代わられる、などの様々な話題が報じられています。
この人工知能という言葉は、知能を持っているかのようなソフトウェアのことを指し示していますが、これは機械学習というプログラミング手法を利用しています。つまり、人口知能の内容を理解するには、機械学習とは何かを理解する必要があります。
機械学習には、次の三つの学習方法があります。
(1) 教師あり学習
(2) 教師なし学習
(3) 強化学習
教師あり学習はコンピュータ(機械)に入力した情報に対し、人がその正解を知っている場合の学習手法で、コンピュータの出力が正解に近づくように学習させます。手書き数字を判別する画像認識や、人が発する音声を理解する音声認識などの場合に利用する学習手法です。
教師なし学習はコンピュータに入力した情報に対し、人がその正解を知らない場合の学習手法です。ある判断ロジックをコンピュータに入れて、そのロジックに基づいて入力情報を処理し、コンピュータに答えを出させます。例えば、ある統計的分布を持つデータの解析では、どのような平均値と分散を持つ正規分布のデータがどのような割合で混ざり合っているか、などを算出します。また、256階調のカラー画像を4色カラーに変換するには、どのような変換式を用いるのが最適か、などを導くことができます。
強化学習はコンピュータに入力した情報に対する正解の出力は分からないが、最終的な正解は分かる場合に利用する学習手法です。例えば、囲碁では最終的な勝ち負けは獲得した領域の広さで決まるので、誰でも簡単に判断できるのですが、その途中段階では、人は正解となる布石を知らないことがほとんどです。そこで途中段階の一手をどこに打つかは、各場所に石を置いた場合の予想勝率をその後の布石を「適当」行って算出し、最も勝率の高い場所として決定します。また、インベーダーゲームでは、直近の連続した数枚の画像をコンピュータに入力しながら、最初はランダムにミサイルの発射の位置とタイミングを選択して、ミサイルを発射し、入力画像と発射の位置・タイミングを成功・不成功と関連づけていきます。これを多数回繰り返すことにより、徐々に成功するミサイル発射の位置・タイミングを学習します。そして最後には人間をも凌ぐ性能を持つようになってきています。
このように機械学習には大きく分けて三種類の学習方法があるので、実現する人工知能の特徴に合わせて適切な機械学習の手法を選ぶことが大切です。
[mathjax]ニューラルネットワークモデルの訓練(training)では、過学習(over-fitting)が起きたり、局所的な極小点に陥り、性能が高くならないという問題が発生することがあります。
過学習
過学習は訓練データの数に対してパラメータの数が多い場合や、訓練データに偏りがある場合に起き易い現象です。図1はデータ数が少ない場合の入出力のグラフ(横軸入力、縦軸出力)ですが、このようにデータ数が少ない場合、各データにほぼ一致する曲線を見出す(パラメータを決定する)ことは難しくありません。
そして、もし図1の数少ないデータが、対象とするデータ全体の分布を代表していいるのであれば、図1の曲線は小さい誤差関数E(前の記事の式(5))を持つ、大域的な最小点に近い、正しい曲線を表していることになります。
しかし、もし図1のデータが、対象とするデータ全体の分布を代表しておらず、データ数を増やすと図2のような分布を示すのであれば、図1の曲線は過学習を表していることになり、正しい曲線は図2のようになります(図1のデータは全て図2に含まれています)。
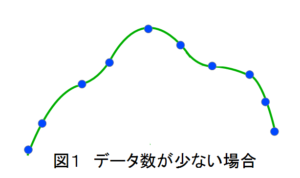
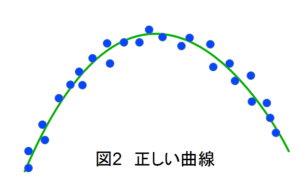
また、パラメータの数が少ない場合には、仮にデータ数が少なくとも、図1に示すような複雑な曲線を出すことは出来ず、単純な曲線になるために、過学習が起きにくいという特徴があります。アナロジーで言えば、図1のデータに対して、パラメータが3つの放物線であれば図2のような曲線が得られますが、パラメータが7個の6次方程式であれば図1のような曲線が得られます。
このように過学習が起きやすいかどうかは、訓練データの数や偏り、パラメータの数に依存します。
局所的な極小点
過学習と同様に、ニューラルネットワークの性能が上がらない原因として、局所的な極小点に陥いることが上げられます。
図3は横軸がパラメータの値を、縦軸がニューラルネットワークの出力を示していますが、図の青●に示す局所的極小点につかまってしまい、学習を継続させてもそこから抜け出すことができず、大域的最小点赤●に到達できないことがよくあります。
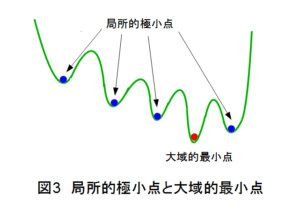
このような過学習や局所的極小点トラップを防ぐ方法として、次の手段がよく使われます。
- 正則化(regularization)
- バッチ処理
- DropoutやDropconnect
<正則化>
正則化は誤差関数E(前の記事の式(5))に罰則項(penalty)を加えたもので、2次のL2ノルムの場合は下記のように表されます。
\[\widetilde { E } \left( w \right) =\frac { 1 }{ 2 } \sum _{ n=1 }^{ N }{ { \left\{ y\left( { x }_{ n },w \right) -{ T }_{ n } \right\} }^{ 2 } } +\frac { \lambda }{ 2 } { \left\| w \right\| }^{ 2 }\qquad (1)\]
ここで、\({ \left\| w \right\| }^{ 2 }={ w }_{ 1 }^{ 2 }+{ w }_{ 2 }^{ 2 }+\quad \cdots \quad +{ w }_{ M }^{ 2 }\)であり、\(\lambda\)は係数で、\(n\)はデータ数、\(m\)はパラメータ数です。
式(1)右辺の罰則項\(w_j^2 , j=1,2,・・・,m\)は2乗で効いてくるので、大きな値を取るとその2乗でエネルギーが増大するため、大きな値とはなりにくくなります。逆に0に近づく力を持ちます。しかし、式(1)右辺第1項の二乗誤差にも\(w_j^2\)の項があり、\(w_j\)はある値(仮にpとする)に近づこうとします。つまり、0に近づこうとする罰則項とpに近づこうとする2乗誤差との綱引きの割合が係数\(\lambda\)で決められています。そのために、pだけに近づこうとする過学習を防ぐ効果が出るのです。L2ノルムの正則化は、意味の無い結合荷重\(w_j\)が減衰しやすいことから、荷重減衰(weight decay)とも呼ばれます。
これに対し1次のL1ノルムでは、罰則項として\(w_j\)の絶対値を加えます。
\[\widetilde { E } \left( w \right) =\frac { 1 }{ 2 } \sum _{ n=1 }^{ N }{ { \left\{ y\left( { x }_{ n },w \right) -{ T }_{ n } \right\} }^{ 2 } } +\frac { \lambda }{ 2 } \sum _{ j=1 }^{ M }{ \left| { w }_{ j } \right| } \qquad (2)\]
L2ノルムとの違いは、\(w_j\)が1乗か2乗かだけです。罰則項だけを次式のように置くと
\[a=\frac {\lambda}{ 2}\sum_{ j=1}^{ M }{ \left|{w}_{j}\right|} \qquad (3)\]
これは\(w_j\)パラメータ空間の直線式を表しています。\(a\)は\(w_j\)軸との交点となります。分かり易い例を上げるならば、\(w_1=x, w_2=y\)として、図4の\(a=|x|+|y|\)という直線を考えてみましょう(図4の緑色直線)。
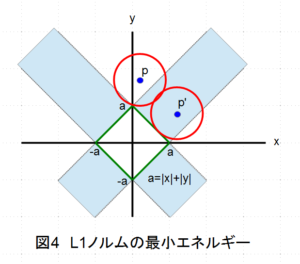
この\(a\)が式(3)の罰則項のエネルギーであり、かつ\(\pm a\)がx軸、y軸の交点となります。つまり緑の正方形の辺の上では、全て同じエネルギー値\(a\)を持つことになります。一方、式(2)右辺の第1項の二乗誤差はpという中心点(青点)を持つ円(赤)の半径rの2乗と考えることができます(厳密には楕円だが、簡単のために円とします)。従って、二乗誤差とL1ノルムを加えた合計エネルギーは\(r^2+a\)と解釈することができます。
赤い円と緑の正方形は同じ\(x,y\)が満足しなければならないので、円と正方形との交点が求める解となります。そして、合計エネルギー\(r^2+a\)を最小にするのは、図4に示したように、正方形に円が接している場合となります。なぜならば、その場合に円の半径rと正方形の切片\(a\)がともに小さくなるからです。
切片\(\pm a\)の正方形と中心pの円が接する条件には、2種類あります。
(1)中心pが図4の白い背景の上にあり正方形の角に接している場合
(2)中心pが図4の薄青色の背景の上にあり正方形の辺に接している場合(p’)
ここで、薄青色の背景は正方形の辺の延長線が囲む領域です。中心pが白い背景の上にある場合には、円が正方形の角に接する場合にエネルギーが最小となりますが、これは\(x=0, y=a\)や\(x=a, y=0\)などを意味しており、パラメータの一方が0になることを示しています。つまり、L1ノルムの正則化を行うとパラメータの一部が確率的に0になり易い傾向がでてきます。それ故に、L1ノルムの導入はスパースモデリングと呼ばれます。
一方、中心pが薄青色の背景の上にある場合(p’)には、パラメータは両方とも0にはならず、\(x=a/2, y=a/2\)などの値を取り得ます。また、0へのドライビングフォースもありません。このように、L1ノルムによる正則化はパラメータの一部が0になる確率が高くなる、というように解釈すべきだと思います。
<バッチ処理、Dropout>
過学習や局所的極小点トラップを防ぐため、言い換えると、ニューラルネットワークの性能を向上させるために、バッチ処理やDropoutも利用されます。
バッチ処理は、逆伝播法による結合荷重の更新を個々のデータに対して行うのではなく、複数のデータに対して一回行う手法です。これは複数のデータに対する平均的な結合荷重で更新するとも言えます。私のこれまでの実験結果から、バッチ処理はニューラルネットワークの性能向上に効くことが多いと言えます。やはり、個々のデータに対して逐一、逆伝播法で結合荷重を更新すると、その変動が大きくなるため、局所的な最小点に捕まり易くなり、大域的な最小点(最適解)に辿り着きにくくなるように思います。
これに対し、バッチ処理では、複数個のデータに対する平均的な結合荷重で更新するために、結合荷重の変動が比較的小さく、滑らかに収束する傾向があり、局所的な極小点に捕まりにくいために、性能低下が抑制されると考えられます。
ただし、データの種類によっては(例えば、ノイズの小さいデータなど)、バッチ処理ではなく、各データで結合荷重を更新した方が更新速度が速く、短時間で収束することもあるので、バッチ処理が常によいとは言えません。そのあたりは、少し注意が必要です。
また、Dropoutはニューラルネットワークのユニットをランダムに排除しながら、結合荷重を更新することで、局所的な極小点のトラップを抑制したり、層数が多くても逆伝播法による結合荷重の更新が入力層付近であっても適切に行われることを狙ったものです。
私もDropoutの性能を調べるために、DeepLearningによるMNISTデータの手書き数字認識に適用してみました。Dropoutなしの認識正解率が98.9%でしたが、Dropoutを導入しても、ほとんど性能は向上せず、むしろ0.1~0.3%ほど性能が下がりました。すでに十分性能が高かったが故に効果がなかったのかもしれません。そうであれば、Dropoutなどは性能が低いニューラルネットワークに対し、効果があるのかもしれない。このあたりはケースバイケースで、ニューラルネットワークの構成を考えていく必要があるようです。
ーーーーーーーー
良書の紹介:機械学習の理解を深めるには良い本です
[mathjax]前の投稿「ニューラルネットワークの基本」に引き続き、バックプロパゲーション(逆伝播)を用いて、重みパラメータとバイアスパラメータを導出する方法について解説します。
最も基本的なニューラルネットワークとして、図1の入力層、隠れ層、出力層で構成された3層構造を考えます(入力層は非線形関数を持たず、ただ入力するだけなので、層としてカウントせず、これを2層構造と言う人もいる)。
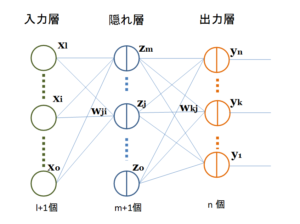
図1.基本的なニューラルネットワークのモデル
〇は非線形活性化関数を持たないユニットを、縦線のある①はこれを持つユニットを表す
入力層の入力データ\(x_i\)の数を \(l\)個、出力データ\(y_k\)数を\(n\)個とすると、入力層と出力層のユニット数は各々 \(l+1\)個、\(n\)個となります。、隠れ層のユニット数は任意に設定することができますが、ここでは\(m+1\)個とします。入力層と隠れ層のユニット数に+1があるのは、バイアスパラメータを意味しています。
また、出力データ\(y_k\)に対応する正解データ\(T_k\)を準備する必要があります。正解データは教師データと呼ばれ、機械学習の結果、出力データを到達させる目標点となります。
それでは、ニューラルネットワークのパラメータ(結合荷重)を計算する方法を説明します。
まず、入力層に入力されたデータ\(x_i\)と隠れ層への入力値\(a_j\)、出力値\(z_j\)と出力層への入力値\(b_k\)、出力値\(y_k\)の間には、前の投稿の式(3)から、次式が得られます。
\[\begin{eqnarray*}
a_j&=&\sum_{i=1}^{l} w_{ji} x_i +w_{j0} \qquad (1)\\
\\z_j&=&f( a_j) \qquad \qquad \qquad (2)\\
\\b_k&=& \sum_{j=1}^{m} w_{kj} z_j +w_{k0} \qquad (3)\\
\\y_k&=&g( b_k) \qquad \qquad \qquad (4)
\end{eqnarray*}\]
ここで、\(f()\)、\(g()\)、\(w_{ji}\)、\(w_{kj}\)は隠れ層と出力層の非線形活性化関数と結合荷重(重みパラメータとバイアスパラメータ)を表しています。\(w_{ji}\)は隠れ層 j 番目のユニットと入力層 i 番目のユニットをつなぐ荷重結合で、\(w_{kj}\)は出力層 k 番目のユニットと隠れ層 j 番目のユニットをつなぐ結合荷重です。
非線形活性化関数として、シグモイド関数やハイパボリックタンジェント関数、Softmax関数が用いられるので、文末にそれらの関数と微分形を整理しておきます。
さて、入力データと正解データからパラメータを算出する目的は、出力値\(y_k\)を教師データ\(T_k\)に近づけることです。従って、出力値\(y_k\)と教師データ\(T_k\)との乖離を示す二乗誤差Eを最少にする結合荷重\(w_{ji}\)、\(w_{kj}\)を求めます。
\[E=\frac { 1 }{ 2 } \sum _{ k=1 }^{ n }{ { \left( { y }_{ k }-{ T }_{ k }\right)}^{ 2 }} \qquad (5)\]
先ず最初に、出力層と隠れ層をつなぐ結合荷重\(w_{kj}\)を、学習率ηを用いて求めます。1回の学習における微小更新量\(\Delta w_{kj}\)を次式のように設定します。
\[\Delta { w }_{ kj }=-\eta \frac {\partial E}{ \partial { w }_{ kj }}\qquad (6)\]
式(6)は一見どのように導出されたのか不思議に思われるかもしれないが、これはただ単に荷重結合\(w_{kj}\)が誤差Eに与える影響∂E/∂\(w_{kj}\)に対し、学習率ηで、Eが小さくなる方向に(-符号をつけて)\(w_{kj}\)を更新する、ということを意味しているに過ぎません。
式(6)は連鎖則(chain rule)により次式のように書くことができます。
\[\Delta { w }_{ kj }=-\eta \frac { \partial E }{ \partial {y}_{k}} \frac { \partial {y}_{k}}{ \partial { b}_{ k } } \frac { \partial { b}_{ k } }{ \partial { w }_{ kj } }\qquad (7)\]
式(7)の各項を見ていきましょう。
式(5)より
\[\frac { \partial E }{ \partial {y}_{k}}=\left( {y}_{k}-{ T }_{ k } \right)\qquad (8)\]
式(4)より
\[\frac { \partial { y }_{ k } }{ \partial { b }_{ k } } =\frac { \partial g\left( { b }_{ k } \right)}{ \partial { b }_{ k } } =g^{ \prime }\left( { b }_{ k } \right) \qquad (9)\]
式(3)より
\[\frac { \partial { b }_{ k } }{ \partial { w }_{ kj } } =\frac { \partial \sum _{ k=1 }^{n}{{w}_{ kj}{ z}_{j}}}{ \partial { w }_{ kj }}={z}_{j}\qquad (10)\]
よって、式(8)、(9)、(10)を用いることで、荷重結合の更新量は次式で表されます。
\[\begin{eqnarray*}\Delta {w}_{kj}&=&-\eta\left({y}_{k}-{T}_{k}\right)g^{\prime}\left({b}_{k}\right)z_j\qquad(11)\\ \\&=&-\eta{\delta}_{k}z_j\qquad(12)\end{eqnarray*}\]
ここで、\(\delta_k = (y_k-T_k)g'(b_k)\)と置き換えています。
以上のように、結合荷重の更新量は式(12)で表されるので、p回学習した結合荷重を\(w_{kj}^p\)で表すと
\[{ w }_{ kj }^{ p+1 }={ w }_{ kj }^{ p }+\Delta { w }_{ kj}\qquad (13)\]
となります。出力\(y_k\)が教師データ\(T_k\)に近づくと、式(11)の荷重結合の更新量も小さくなり、収束に向かうことが分かります。
次に、隠れ層と入力層の間の荷重結合の微小更新量\(\Delta w_{ji}\)を式(6)と同様に設定します。
\[\Delta { w }_{ ji }=-\eta \frac {\partial E}{ \partial { w }_{ ji }}\qquad (14)\]
隠れ層からの出力\(z_j\)は出力層の全てのユニットに広がって連結された後に、誤差Eに影響するために、連鎖則(Chain Rule)では、連結されている全てのユニットを考慮して、式(14)は次式のように展開します。
\[\begin{eqnarray*}\Delta { w }_{ ji }&=&-\eta \frac { \partial E}{ \partial { z }_{ j } }\frac { \partial { z }_{ j } }{ \partial { a }_{ j } } \frac { \partial { a }_{ j } }{ \partial { w }_{ ji } }\\ \\&=&-\eta \frac { \partial \left\{ \sum _{ k=1 }^{ n }{ { E }}\right\} }{ \partial { z }_{ j } }\frac { \partial { z }_{ j } }{ \partial { a }_{ j } } \frac { \partial { a }_{ j } }{ \partial { w }_{ ji } }\\ \\&=&-\eta \left\{ \sum _{ k=1 }^{ n }{ \frac { \partial E }{ \partial { z }_{ j } }}\right\} \frac { \partial { z }_{ j } }{ \partial { a }_{ j } } \frac { \partial { a }_{ j } }{ \partial { w }_{ ji } }\qquad (15)\\ \\&=&-\eta \left\{ \sum _{ k=1 }^{ n }{ \frac { \partial E }{ \partial { y }_{ j }}\frac { \partial { y }_{ j } }{ \partial { b }_{ j } } \frac { \partial { b }_{ j }}{ \partial { z }_{ j } }}\right\} \frac { \partial { z }_{ j } }{ \partial { a }_{ j } } \frac { \partial { a }_{ j } }{ \partial { w }_{ ji } } \qquad (16)\end{eqnarray*}\]
式(16)の各項を見ていきます。
式(8)より、\(\partial E/\partial y_k\)が、式(9)より、\(\partial y_k/\partial b_k\)が得られ、また
\[\frac { \partial { b }_{ k } }{ \partial { z }_{ j }} =\frac { \partial \sum _{ k=1 }^{ n }{{w}_{ kj }{z}_{k}}}{ \partial {z}_{j}}={w}_{ kj }\qquad (17)\]
となる。式(2)より
\[\frac { \partial { z }_{ j } }{ \partial { a }_{ j } } =\frac { \partial f\left( { a }_{ j } \right)}{ \partial { a }_{ j } } =f^{ \prime }\left( { a }_{ j } \right)\qquad (18)\]
となり、式(16)の最後の項は
\[\frac { \partial { a }_{ j } }{ \partial { w }_{ ji } } =\frac { \partial \sum _{ i=1 }^{ l }{ { w }_{ ji }{ x }_{ i } }}{ \partial { w }_{ ji } } ={ x }_{ i }\qquad (19)\]
となる。よって
\[\Delta { w }_{ ji }=-\eta \left\{ \sum _{ k=1 }^{ n }{ \left( { y }_{ k }-{ T }_{ k } \right) g^{\prime}\left( { b }_{ k } \right) { w }_{ kj } } \right\} f^{ \prime }\left( { z }_{ j } \right) { x }_{ i }\qquad (20)\\ =-\eta \left\{ \sum _{ k=1 }^{ n }{ { w }_{ kj }{ \delta}_{k}}\right\} f^{\prime}\left( { z }_{ j } \right) { x }_{ i }\qquad (21)\]
\[ =-\eta { \delta}_{j}{ x }_{ i }\qquad (22)\]
のように荷重結合の更新量が得られました。ただし、ここでは次式を利用しています。
\[{ \delta }_{ j }=f^{ \prime }\left( { z }_{ j } \right) \sum _{ k=1 }^{ n }{ { w }_{ kj }{ \delta}_{ k } } \qquad (23)\]
従って、式(13)と同様に、p回の更新によって、入力層と隠れ層の間の荷重結合\(w_{ji}^p\)は、次式のように表されます。
\[{ w }_{ ji }^{ p+1 }={ w }_{ ji }^{ p }+\Delta { w }_{ ji }\qquad (24)\]
式(13)と合わせると、全ての結合荷重が算出できました。これがニューラルネットワークの誤差逆伝播で行うパラメータ更新の内容です。
多くのデータを用いて学習させ、結合荷重を収束させて、決定することが出来たならば、それを用いてニューラルネットワークの式(1)~(4)を構築します。そして、新たな入力データに対してフィードフォワードの計算することで、簡単に出力を得ることができます。その出力は、新たな入力データを過去データに基づいて判断した答えというになります。
ただ、学習用のデータセットに対しては式(5)の誤差Eが局所的極小点(Local Minimum)に落ち込み比較的小さい値を示すものの、その後の新規データに対してはEの値が大きく、結果がよくないことがしばしば起こります。これを過学習(overfitting)と言います。この過学習を防ぐための工夫について、次回お話します。
---------------------------
<お勧め書籍>
機械学習について丁寧に書かれた良書です。本格的に勉強したい人には必携のお勧め本です。
良書の紹介:機械学習の理解を深めるには良い本です
======== 非線形活性化関数 ========
シグモイド関数
\[h\left( x \right) =\frac { 1 }{ 1+exp\left( -x \right)}\qquad (a1)\]
\[\frac { \partial h\left( x \right)}{ \partial x } =h\left( x \right) \left( 1-h\left( x \right) \right) \qquad (a2)\]
ハイパボリックタンジェント関数
\[h\left( { x } \right) =tanh\left( x \right)=\frac { exp\left( x \right) -exp\left( -x \right)}{ exp\left( x \right) +exp\left( -x \right)}\qquad (a3)\]
\[\frac { \partial h\left( x \right)}{ \partial x } =1-h\left( x \right) \cdot h\left( x \right)\qquad (a4)\]
Softmax関数
\[h\left( { x } \right) =\frac { exp\left( { x }_{ i } \right)}{ \sum _{ j=1 }^{ n }{ exp\left( { x }_{ j } \right)}}\qquad (a5)\]
\[\frac { \partial h\left( { { x }_{ i } } \right)}{ \partial { x }_{ i } } =h\left( { x }_{ i } \right) \qquad (a6)\]
Softmax関数はその層にある全ユニットの出力値の合計を分母とし、注目ユニットの出力を分子に持っています。これは全てのユニットの出力合計を1に規格化するためであり、出力を確率に変換する際などに利用されます。