[mathjax]人工知能の代表的な技術の一つに人工ニューラルネットワーク(Artificial Neural Network)があります。
人工ニューラルネットワークは、脳の神経細胞ニューロンの構造を真似て作成したもので、複数のニューロンが存在する層を積層し、異なる層のニューロンを接続して信号を伝達します。
今、\(p\)番目の層(\(p\)層とする)の\(j\)番目のユニット(ニューロン)について考えます。\(p-1\)層の\(i\)番目のユニットの出力を\(x_i\)とすると、これに重みパラメータ\(w_{ji}^{(p)}\)を乗じた項の線形和\(a_j\)が\(p\)層の\(j\)番目のユニットへの入力となります。
\[a_j= \sum_{i=0}^{m} w_{ji}^{(p)}x_i \qquad (1)\]
ここで、\(w_{ji}^{(p)}\)は\(p-1\)層の\(i\)番目のユニットから\(p\)層の\(j\)番目のユニットへの重みパラメータ\(w\)を表しており、\(a_j\)は活性と呼ばれます。
そして、\(p\)層、\(j\)番目のユニットへの入力\(a_j\)は、微分可能な非線形活性化関数\(h()\)により出力\(z_j\)に変換されます。
\[z_j=h(a_j) \qquad (2)\]
ここでは\(i=0\)の時、\(x_0=1\)として、入力信号の影響を受けない項\(w_{j0}^{(p)}\)としています。これをバイアスパラメータと呼びます。
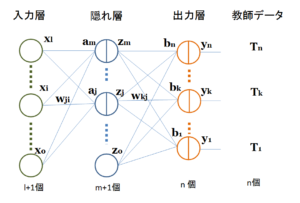
図1 ニューラルネットワークの構成図
重みパラメータとバイアスパラメータを区別し、式(1)、(2)をまとめて書くと、
\[z_j=h( \sum_{i=1}^{m} w_{ji}^{(p)}x_i +w_{j0}^{(p)}) \qquad (3)\]
となり、\(p\)層の\(j\)番目のユニットへの入力\(x_i\)と出力\(z_j\)が表されます。
図1では、\(p-1\)層の全てのユニットから\(p\)層の\(j\)番目のユニットへの接続線しか表示されていないのですが、\(p-1\)層の全てのユニットは\(p\)層の全てのユニットに接続されています。
そして、重みパラメータとバイアスパラメータの値、および非線形活性化関数により、入力を所望の出力に変換させることを狙いとしています。
非線形活性化関数\(h()\)には、ロジステックシグモイド関数やtanh関数などのシグモイド関数が利用されます。
ロジステックシグモイド関数 \(\sigma\left(\right)\)
\[\sigma \left( a_j \right) =\frac { 1 }{ 1+exp\left({ -a_j }\right) } \qquad (4)\]
ハイパーボリックタンジェント関数 \(tanh\left(\right)\)
\[tanh \left( a_j \right) =\frac { exp\left({ a_j }\right)-exp\left({ -a_j }\right) }{ exp\left({ a_j }\right)+exp\left({ -a_j }\right) } \qquad (5)\]
式(3)の出力\(z_j\)は次の層への入力信号となり、順次これが繰り返され、最終的な出力が得られます。
分かり易い例として、図1のような、\(p-1\)層が入力層で、\(p\)層が隠れ層、\(p+1\)層が出力層となる3層構造を考えてみましょう。
これを用いて、例えば、30画素×30画素の白黒画像の数字0~9を認識させる場合であれば、入力層のユニット数を900個とし、ここに900画素の輝度値を入力します。つまり、輝度値が図1の\(x_i\)となります。ただし、輝度値\(x_i\)は0~1の間に収まるように規格化するのが一般的です。そして、式(3)を用いて隠れ層の出力\(z_j\)を計算します。この出力が3番目の出力層への入力信号となります。
隠れ層のユニット数は自由に設定することができます。言い換えると、性能が良くなるユニット数を実験から見出さねばなりません。
出力層のユニット数は10個とし、数字の0~9に対応させます。そして、例えば、数字の2の画像(900画素の輝度値)を入力したら、その正解出力は、出力層の2番目のユニットが1となり、その他は0となります。数字の5であれば、正解出力は出力層の5番目のユニットが1となり、その他は0となります。このような正解出力が出るように重みパラメータとバイアスパラメータを決定します。正解出力から逆方向に遡ってパラメータを決める過程をバックプロパゲーションと呼びます。また、0~9までの数字画像を次々と入力し、正解出力を与えて、その計算過程にあるパラメータを決めるプロセスは、まるで機械が学習をしているようなので、機械学習と呼ばれます。
次回は、バックプロパゲーションによりパラメータを算出する方法を解説します。