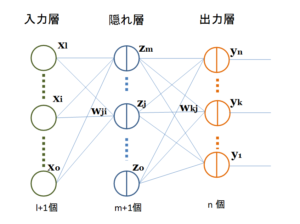
[mathjax]ニューラルネットワークモデルの訓練(training)では、過学習(over-fitting)が起きたり、局所的な極小点に陥り、性能が高くならないという問題が発生することがあります。
過学習
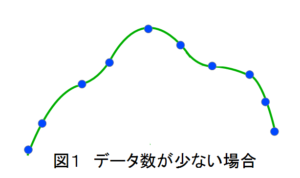
過学習は訓練データの数に対してパラメータの数が多い場合や、訓練データに偏りがある場合に起き易い現象です。図1はデータ数が少ない場合の入出力のグラフ(横軸入力、縦軸出力)ですが、このようにデータ数が少ない場合、各データにほぼ一致する曲線を見出す(パラメータを決定する)ことは難しくありません。
そして、もし図1の数少ないデータが、対象とするデータ全体の分布を代表していいるのであれば、図1の曲線は小さい誤差関数E(前の記事の式(5))を持つ、大域的な最小点に近い、正しい曲線を表していることになります。
しかし、もし図1のデータが、対象とするデータ全体の分布を代表しておらず、データ数を増やすと図2のような分布を示すのであれば、図1の曲線は過学習を表していることになり、正しい曲線は図2のようになります(図1のデータは全て図2に含まれています)。
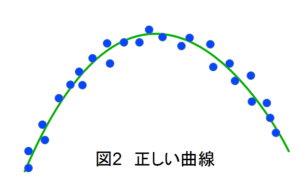
また、パラメータの数が少ない場合には、仮にデータ数が少なくとも、図1に示すような複雑な曲線を出すことは出来ず、単純な曲線になるために、過学習が起きにくいという特徴があります。アナロジーで言えば、図1のデータに対して、パラメータが3つの放物線であれば図2のような曲線が得られますが、パラメータが7個の6次方程式であれば図1のような曲線が得られます。
このように過学習が起きやすいかどうかは、訓練データの数や偏り、パラメータの数に依存します。
局所的な極小点
過学習と同様に、ニューラルネットワークの性能が上がらない原因として、局所的な極小点に陥いることが上げられます。
図3は横軸がパラメータの値を、縦軸がニューラルネットワークの出力を示していますが、図の青●に示す局所的極小点につかまってしまい、学習を継続させてもそこから抜け出すことができず、大域的最小点赤●に到達できないことがよくあります。
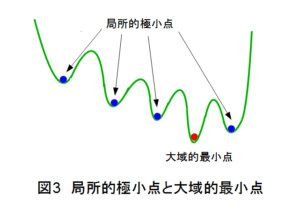
このような過学習や局所的極小点トラップを防ぐ方法として、次の手段がよく使われます。
- 正則化(regularization)
- バッチ処理
- DropoutやDropconnect
<正則化>
正則化は誤差関数E(前の記事の式(5))に罰則項(penalty)を加えたもので、2次のL2ノルムの場合は下記のように表されます。
\[\widetilde { E } \left( w \right) =\frac { 1 }{ 2 } \sum _{ n=1 }^{ N }{ { \left\{ y\left( { x }_{ n },w \right) -{ T }_{ n } \right\} }^{ 2 } } +\frac { \lambda }{ 2 } { \left\| w \right\| }^{ 2 }\qquad (1)\]
ここで、\({ \left\| w \right\| }^{ 2 }={ w }_{ 1 }^{ 2 }+{ w }_{ 2 }^{ 2 }+\quad \cdots \quad +{ w }_{ M }^{ 2 }\)であり、\(\lambda\)は係数で、\(n\)はデータ数、\(m\)はパラメータ数です。
式(1)右辺の罰則項\(w_j^2 , j=1,2,・・・,m\)は2乗で効いてくるので、大きな値を取るとその2乗でエネルギーが増大するため、大きな値とはなりにくくなります。逆に0に近づく力を持ちます。しかし、式(1)右辺第1項の二乗誤差にも\(w_j^2\)の項があり、\(w_j\)はある値(仮にpとする)に近づこうとします。つまり、0に近づこうとする罰則項とpに近づこうとする2乗誤差との綱引きの割合が係数\(\lambda\)で決められています。そのために、pだけに近づこうとする過学習を防ぐ効果が出るのです。L2ノルムの正則化は、意味の無い結合荷重\(w_j\)が減衰しやすいことから、荷重減衰(weight decay)とも呼ばれます。
これに対し1次のL1ノルムでは、罰則項として\(w_j\)の絶対値を加えます。
\[\widetilde { E } \left( w \right) =\frac { 1 }{ 2 } \sum _{ n=1 }^{ N }{ { \left\{ y\left( { x }_{ n },w \right) -{ T }_{ n } \right\} }^{ 2 } } +\frac { \lambda }{ 2 } \sum _{ j=1 }^{ M }{ \left| { w }_{ j } \right| } \qquad (2)\]
L2ノルムとの違いは、\(w_j\)が1乗か2乗かだけです。罰則項だけを次式のように置くと
\[a=\frac {\lambda}{ 2}\sum_{ j=1}^{ M }{ \left|{w}_{j}\right|} \qquad (3)\]
これは\(w_j\)パラメータ空間の直線式を表しています。\(a\)は\(w_j\)軸との交点となります。分かり易い例を上げるならば、\(w_1=x, w_2=y\)として、図4の\(a=|x|+|y|\)という直線を考えてみましょう(図4の緑色直線)。
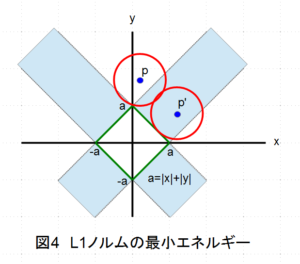
この\(a\)が式(3)の罰則項のエネルギーであり、かつ\(\pm a\)がx軸、y軸の交点となります。つまり緑の正方形の辺の上では、全て同じエネルギー値\(a\)を持つことになります。一方、式(2)右辺の第1項の二乗誤差はpという中心点(青点)を持つ円(赤)の半径rの2乗と考えることができます(厳密には楕円だが、簡単のために円とします)。従って、二乗誤差とL1ノルムを加えた合計エネルギーは\(r^2+a\)と解釈することができます。
赤い円と緑の正方形は同じ\(x,y\)が満足しなければならないので、円と正方形との交点が求める解となります。そして、合計エネルギー\(r^2+a\)を最小にするのは、図4に示したように、正方形に円が接している場合となります。なぜならば、その場合に円の半径rと正方形の切片\(a\)がともに小さくなるからです。
切片\(\pm a\)の正方形と中心pの円が接する条件には、2種類あります。
(1)中心pが図4の白い背景の上にあり正方形の角に接している場合
(2)中心pが図4の薄青色の背景の上にあり正方形の辺に接している場合(p’)
ここで、薄青色の背景は正方形の辺の延長線が囲む領域です。中心pが白い背景の上にある場合には、円が正方形の角に接する場合にエネルギーが最小となりますが、これは\(x=0, y=a\)や\(x=a, y=0\)などを意味しており、パラメータの一方が0になることを示しています。つまり、L1ノルムの正則化を行うとパラメータの一部が確率的に0になり易い傾向がでてきます。それ故に、L1ノルムの導入はスパースモデリングと呼ばれます。
一方、中心pが薄青色の背景の上にある場合(p’)には、パラメータは両方とも0にはならず、\(x=a/2, y=a/2\)などの値を取り得ます。また、0へのドライビングフォースもありません。このように、L1ノルムによる正則化はパラメータの一部が0になる確率が高くなる、というように解釈すべきだと思います。
<バッチ処理、Dropout>
過学習や局所的極小点トラップを防ぐため、言い換えると、ニューラルネットワークの性能を向上させるために、バッチ処理やDropoutも利用されます。
バッチ処理は、逆伝播法による結合荷重の更新を個々のデータに対して行うのではなく、複数のデータに対して一回行う手法です。これは複数のデータに対する平均的な結合荷重で更新するとも言えます。私のこれまでの実験結果から、バッチ処理はニューラルネットワークの性能向上に効くことが多いと言えます。やはり、個々のデータに対して逐一、逆伝播法で結合荷重を更新すると、その変動が大きくなるため、局所的な最小点に捕まり易くなり、大域的な最小点(最適解)に辿り着きにくくなるように思います。
これに対し、バッチ処理では、複数個のデータに対する平均的な結合荷重で更新するために、結合荷重の変動が比較的小さく、滑らかに収束する傾向があり、局所的な極小点に捕まりにくいために、性能低下が抑制されると考えられます。
ただし、データの種類によっては(例えば、ノイズの小さいデータなど)、バッチ処理ではなく、各データで結合荷重を更新した方が更新速度が速く、短時間で収束することもあるので、バッチ処理が常によいとは言えません。そのあたりは、少し注意が必要です。
また、Dropoutはニューラルネットワークのユニットをランダムに排除しながら、結合荷重を更新することで、局所的な極小点のトラップを抑制したり、層数が多くても逆伝播法による結合荷重の更新が入力層付近であっても適切に行われることを狙ったものです。
私もDropoutの性能を調べるために、DeepLearningによるMNISTデータの手書き数字認識に適用してみました。Dropoutなしの認識正解率が98.9%でしたが、Dropoutを導入しても、ほとんど性能は向上せず、むしろ0.1~0.3%ほど性能が下がりました。すでに十分性能が高かったが故に効果がなかったのかもしれません。そうであれば、Dropoutなどは性能が低いニューラルネットワークに対し、効果があるのかもしれない。このあたりはケースバイケースで、ニューラルネットワークの構成を考えていく必要があるようです。
ーーーーーーーー
良書の紹介:機械学習の理解を深めるには良い本です